Grant Stagg

I build algorithms for safe autonomous flight in contested environments. My research focuses on probabilistic engagement zones, uncertainty propagation, and real-time path planning under adversarial conditions.

Summary

This paper presents the Curve–Straight Probabilistic Engagement Zone (CSPEZ), a probabilistic model for assessing capture risk in adversarial environments. It models the region an evader should avoid to remain safe from a Dubins-style pursuer whose parameters—such as position, heading, speed, and turn rate—are uncertain. The work builds on an analytic model of the Curve–Straight Basic Engagement Zone (CSBEZ) and extends it using uncertainty propagation and learning-based methods.

Key contributions include:

  • A closed-form analytic solution for the CSBEZ, assuming a curve-straight pursuer path.
  • Four CSPEZ approximation methods: Monte Carlo, linear, quadratic, and neural network.
  • A path planning algorithm that incorporates CSPEZ constraints to enable safe trajectory generation under uncertainty.
  • Extensive comparisons of approximation accuracy, efficiency, and application to real-time planning.

Figures

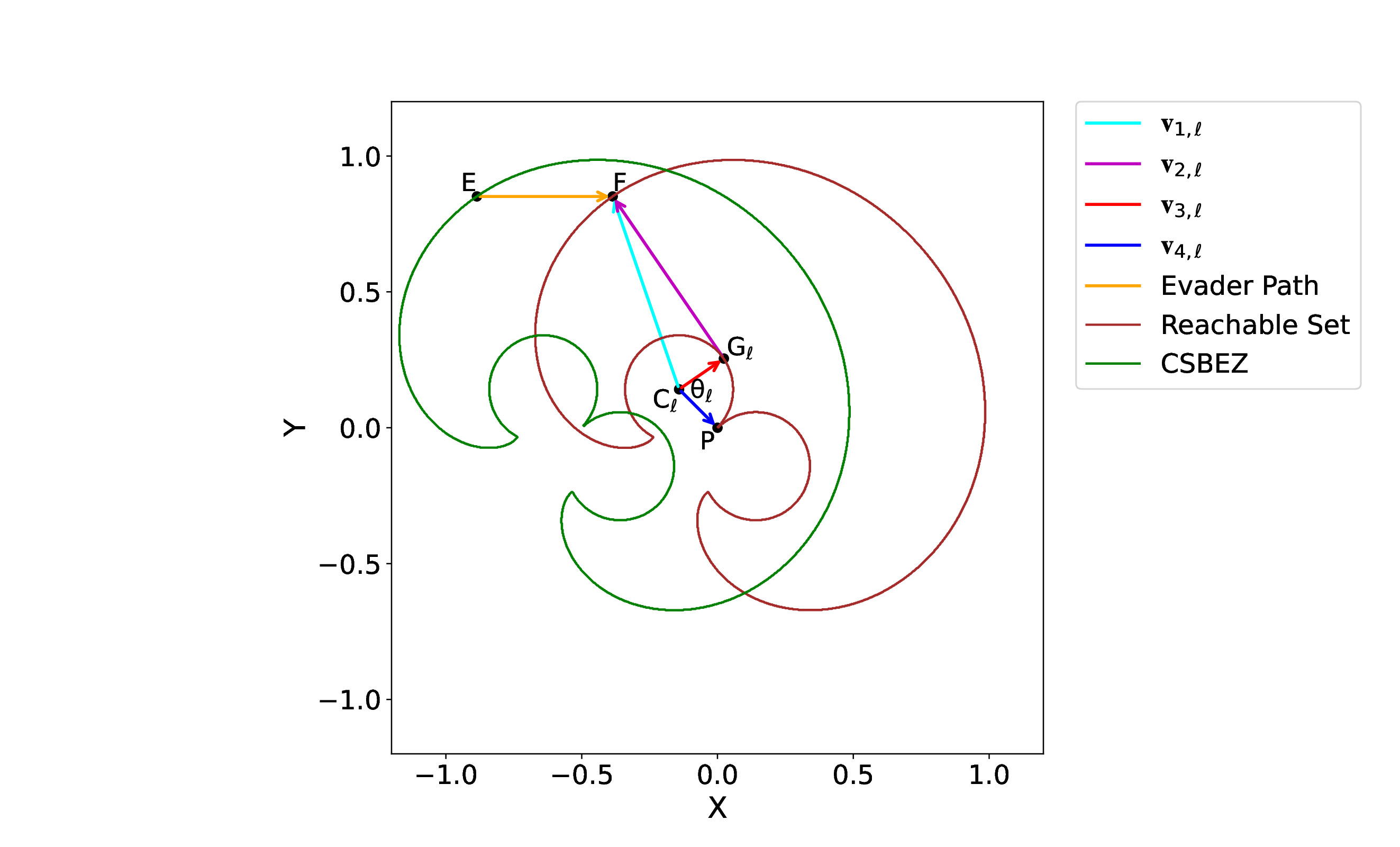
CSBEZ Boundary

Figure: The CSBEZ boundary for a Dubins-style pursuer with known parameters.

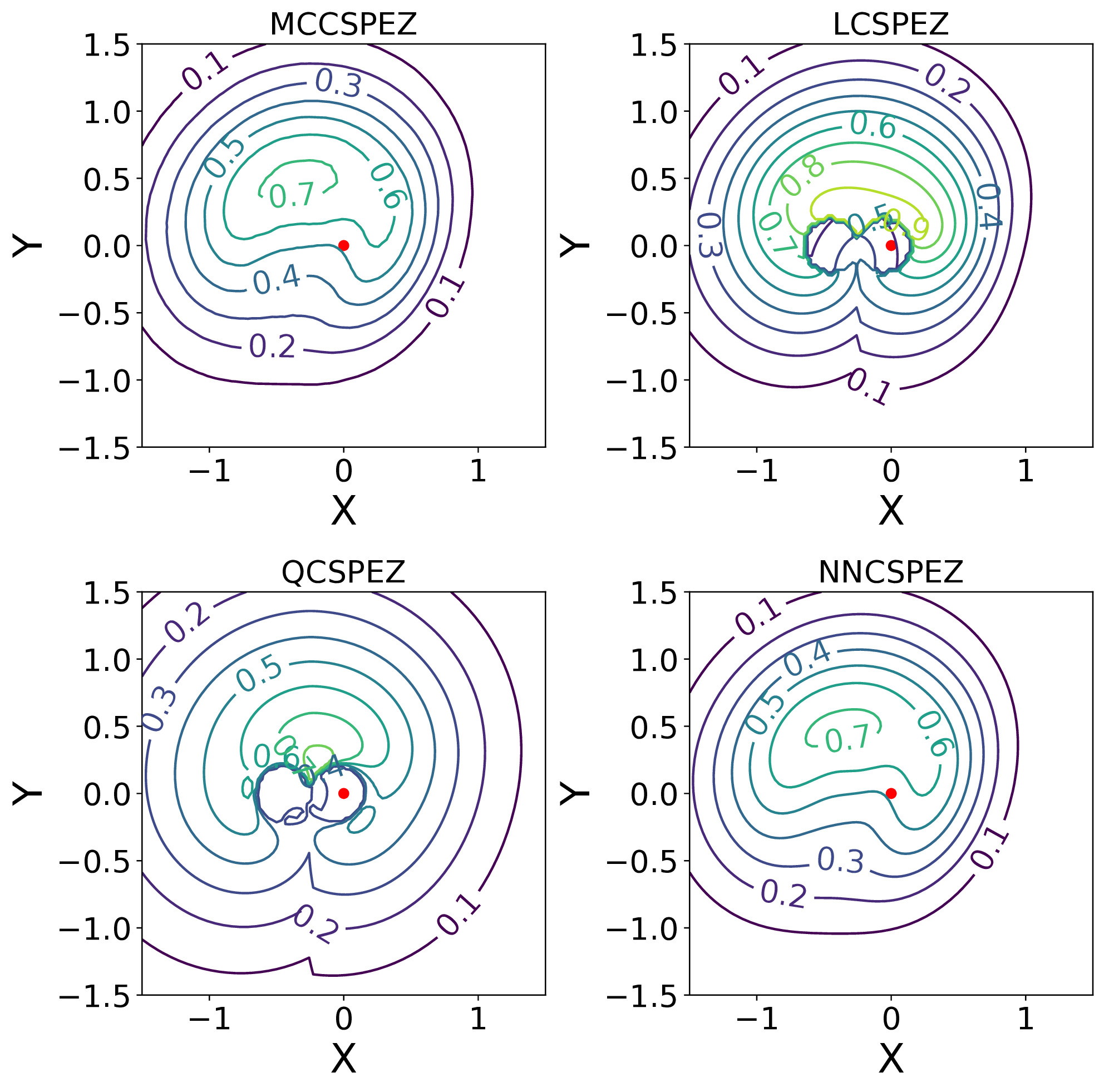
CSPEZ Approximation Example

Figure: CSPEZ probability contours using different approximation methods.

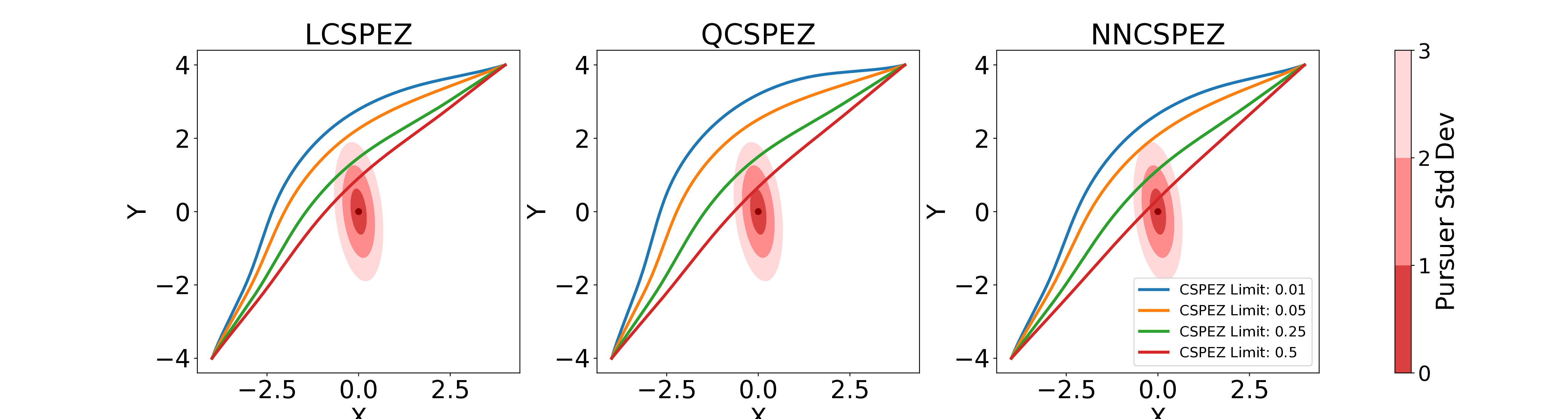
CSPEZ Path Planneing

Figure: Paths planned using the different CSPEZ approximation methods as safety constraints. The safer the path (lower probability of being inside true CSBEZ), the further the path skirts around the pursuer.

Abstract

Curve–straight probabilistic engagement zones (CSPEZ) quantify spatial regions an evader should avoid to mitigate capture risk against a turn-rate limited pursuer performing a curve–straight path with uncertain parameters (position, heading, velocity, range, and maximum turn rate). This research presents strategies and algorithms for generating evader paths that minimize capture risk from a pursuer when such uncertainty exists. We begin by deriving an analytic solution for the deterministic curve–straight engagement zone (CSBEZ). We then extend this model into a probabilistic framework by conducting a sensitivity analysis using Monte Carlo sampling, linearization, quadratic approximation, and neural network regression to account for parameter uncertainty. The accuracy, memory usage, and computational cost of these methods are evaluated in simulation. Finally, we incorporate CSPEZ constraints into a path planning algorithm to generate safe trajectories that explicitly consider pursuer uncertainty.

Citation

Stagg, Grant; Peterson, Cameron K.; and Weintraub, Isaac.
“Probabilistic Weapon Engagement Zones for a Turn-Constrained Pursuer.”
Submitted to AIAA Journal of Aerospace Information Systems, 2024.
[PDF Coming Soon]