Grant Stagg

I build algorithms for safe autonomous flight in contested environments. My research focuses on probabilistic engagement zones, uncertainty propagation, and real-time path planning under adversarial conditions.

Summary

This paper introduces the concept of Probabilistic Engagement Zones (PEZs) — a framework for estimating the likelihood that an agent is inside an adversary’s engagement zone when the adversary’s parameters are uncertain. Basic weapon engagement zones (BEZs) define configurations (position and heading) and evader should avoid if they wish to avoid being nuetralized by an adversary. Traditional BEZ models fail to account for pursuer parameter uncertainty; PEZs resolve this by propagating uncertainty through the BEZ boundary using a linearization approach. The PEZ model is then integrated into a trajectory optimization problem, providing a tunable safety constraint for adversarial path planning.

Key contributions:

  • Introduced the PEZ as a probability-aware generalization of BEZs
  • Developed linearized PEZ to account for uncertainty in pursuer parameters.
  • Integrated PEZ constraints into a trajectory optimization algorithm.

Figure

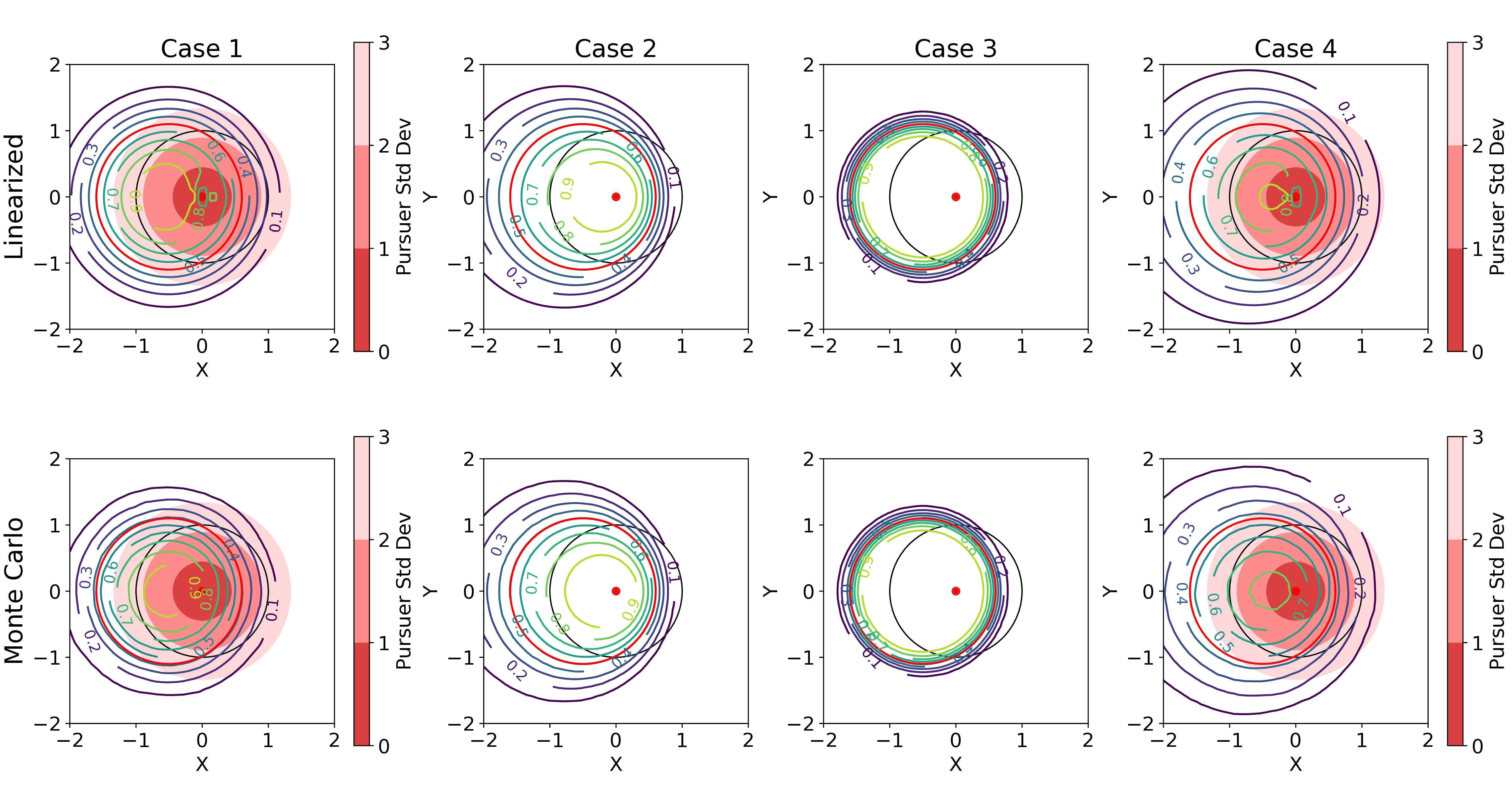
Linearized PEZ

Figure: Level sets of probability of being inside the true engagement zone generated using Monte Carlo and linearized PEZ.

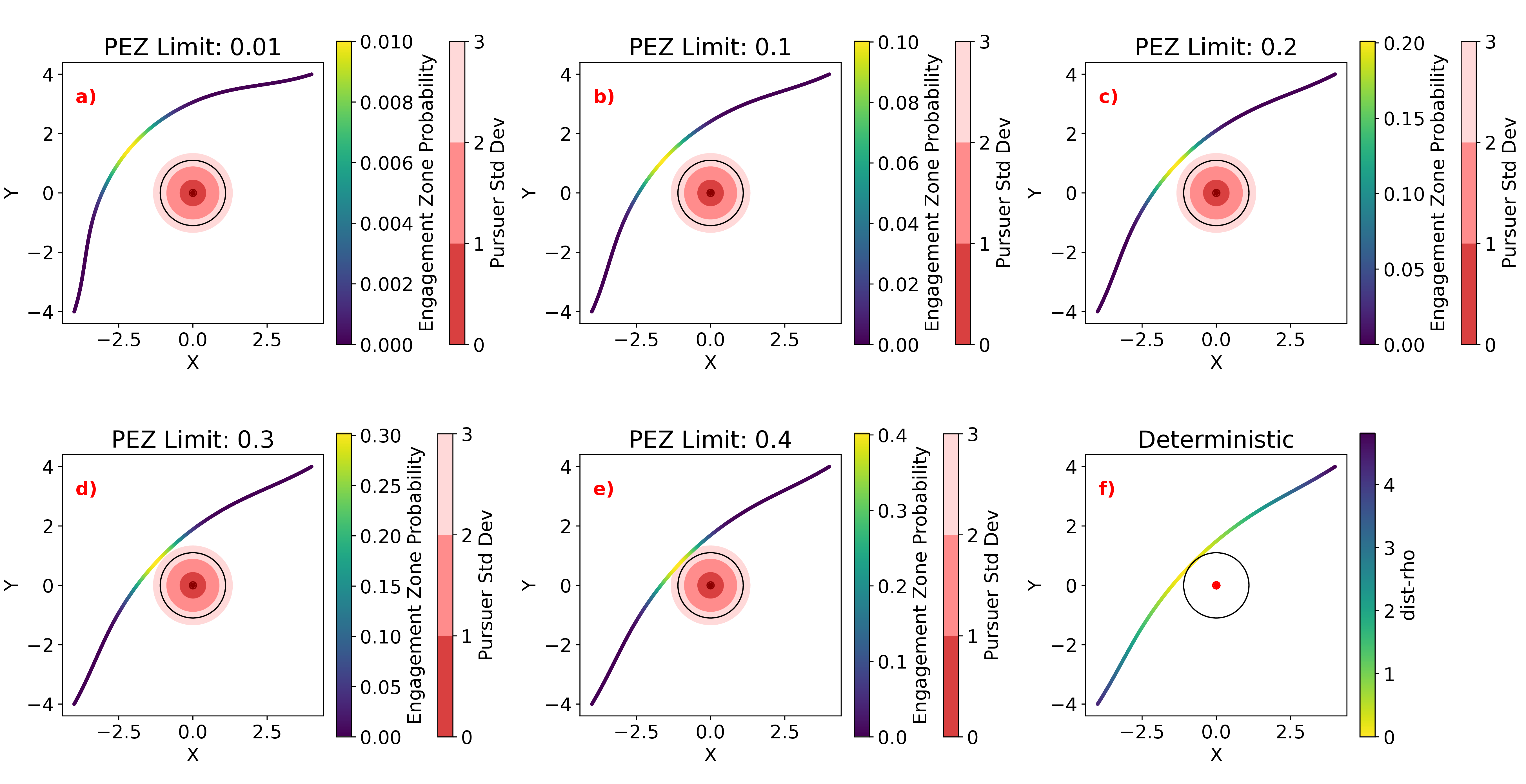
PEZ path planning

Figure: Paths generated using linearized PEZ as a safety constraint. Various safety thresholds are shown

Abstract

In this work, we present linearized probabilistic weapon engagement zones (linearized PEZ), which provide a method to prevent agents from engaging in a pursuer-evasion differential game while accounting for uncertainty in the parameters of the game. This type of differential game is commonly used to model adversarial environments, where the parameters of the adversary (pursuer), such as initial positions and range, are often unknown or uncertain. Additionally, with the increasing potential of GPS jamming in modern warfare, even friendly (evader) parameters, such as position and orientation, can be uncertain. We demonstrate that linearized PEZ effectively approximates the true engagement zone distribution found using a Monte Carlo method. Using linearized PEZ, we develop a path optimization algorithm that plans safe trajectories while addressing this uncertainty. Numerical simulations are presented to demonstrate the effectiveness of our approach.

Citation

G. Stagg and C. K. Peterson,
“Probabilistic Weapon Engagement Zones”
2025 American Control Conference (ACC).
Link to Article PDF